本文的目的是向你讲述1997年奥斯卡获奖电影《心灵捕手》中的虚构人物威尔（Will）解决的两个数学问题。

电影中的情节

《心灵捕手》讲述了虚构人物威尔·亨特的故事，尽管他拥有非凡的智慧，但他却在波士顿的麻省理工学院担任清洁工。有一天，他在走廊的黑板上发现了一个由菲尔兹奖获奖教授杰拉尔德·兰博（Gerald Lambeau）提出的问题。威尔拥有超强的记忆力，他记住了这个问题，并在家中浴室的镜子上解决了它。第二天回到麻省理工学院，他忍不住在黑板上匿名地写出了他的答案。

第二天，教授提出了另一个更难的问题。威尔再次解决了它，但当他写解题过程时被教授抓住了，教授震惊地发现麻省理工最聪明的年轻数学家是一个没有受过教育的清洁工。

第一个问题

• 杰拉尔德·兰博教授审阅威尔写出的解题过程。

问题1：给定图G，求：

1. 邻接矩阵A（在图论和计算机科学中，邻接矩阵是用来表示有限图的一个方阵。矩阵的元素表示图中顶点对是否相邻。）
2. 找出长度为3的路径数的矩阵
3. 从i到j的路径数的生成函数
4. 从1到3的路径数的生成函数

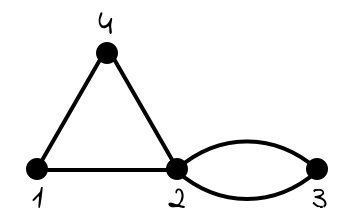
• 图1：图G

第一个问题，在图论中，求图G中顶点i到顶点j的路径数。为此，设G是一个顶点集合V ={1，2，3，4}的图，和边E ={(1、2)，(1,4)，(2、4)，(2、3)，(2,3)}，其中(2、3)是一个双边。

问题1的解

邻接矩阵是用来表示有限图的一个方阵。邻接矩阵L的元素表示图中顶点对是否相邻。对于一个具有一组顶点V的简单图（一个自环是两个端点为同一顶点的边。如果有多于一条边连接同一对顶点，则它们均被称为重边。一个图的重数是重复次数最多的边的重复次数。如果一个图不含自环或重边，则称为简单图），邻接矩阵是一个正方形|L| × |L|矩阵，当顶点i到顶点j有一条边时，其元素L_ij为1；当顶点i到顶点j有两条边时，其元素L_ij为2；当顶点i到顶点j没有边时L_ij为0。矩阵的对角线元素都是零，因为在简单图中不允许从顶点i到自身（循环）的边。对于沿边集E的所有长度为1的路径，这给了我们如下图G的邻接矩阵：

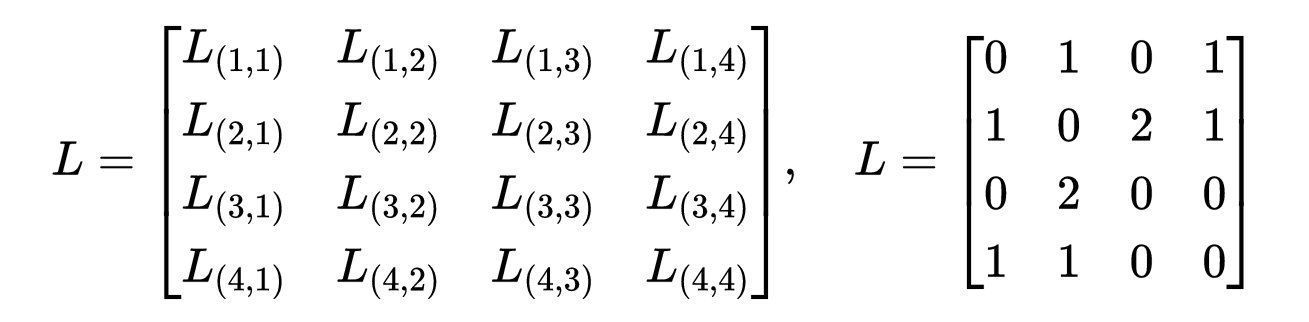
• 问题1.1的解。顶点i到j的边元素和图G的邻接矩阵，表示顶点i到j之间的边数

问题1.2是找出一个矩阵，编码了长度为3的路径的所有可能情况。从i到j的n + 1步路径包括从i到k的n步路径和从k到j的1步路径。也就是说，L??1的ij项由下面的和给出：

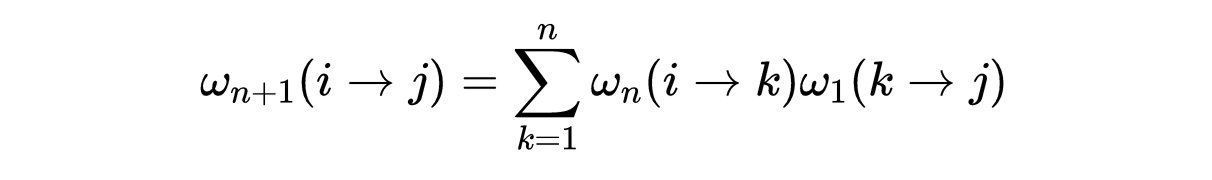
• 方程1

例如，对于k = 1，2：

1. 从顶点i到顶点j的路径，长度为3；
2. 从顶点i到k的路径，长度为2；
3. 从顶点k到j的路径，长度为1。

通过矩阵乘法，对于从i到j的所有长度为3的路径，给出了以下矩阵：

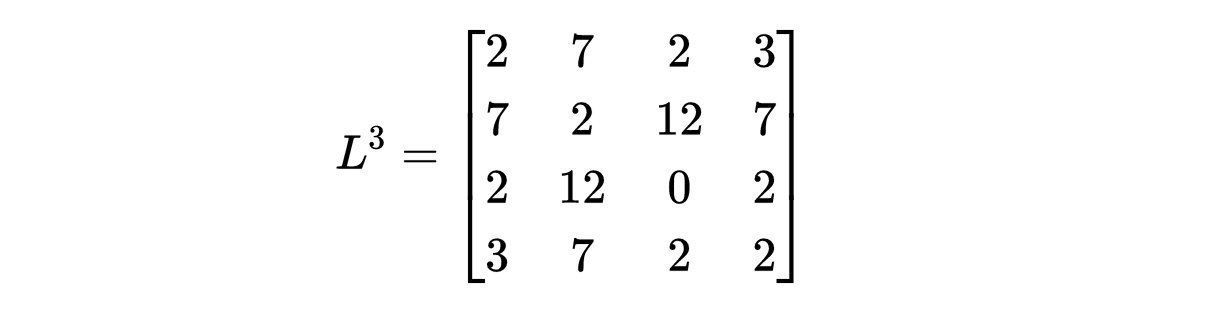
• 问题1.2的解。表示图G中顶点i到j长度为3的路径数的矩阵

问题1.3要求从顶点i到j的生成函数。为了回答这个问题，霍瓦特（Horváth）等人考虑一个由幂级数定义的解析生成函数：

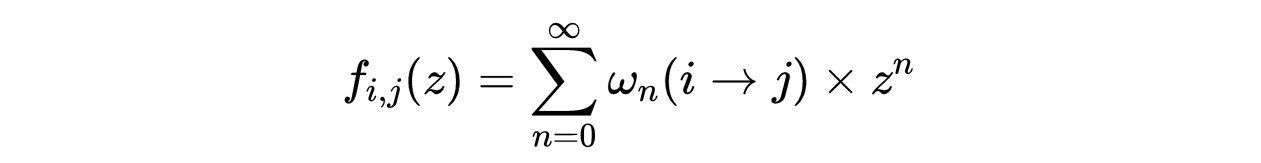
• 方程2

其中系数z^n表示从i到j的路径数为n的数目。从问题1.3中，我们发现ω_n（i→j）是矩阵L^n的ij项。这个问题要求生成能同时给出所有项的生成函数，因此考虑由我们熟悉的幂级数给出的矩阵L是有意义的：

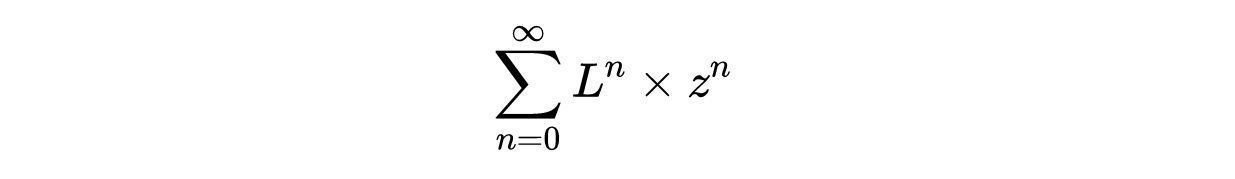
• 方程3

其中L^n是包含从每个顶点i到j的路径数的数目的矩阵（解决问题1.2的一般情况）。可以用常见的几何幂级数恒等式来计算求和，即：

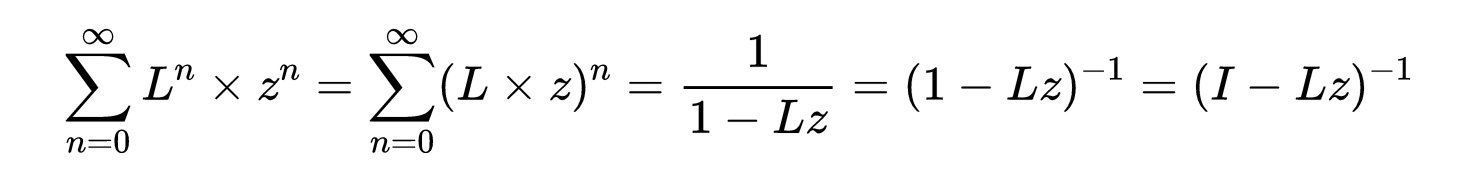
• 方程4

为了计算(I?z × L)的逆，我们可以使用克莱默法则。设M_ij为去除M的第i列和第j行得到的矩阵,得到一个矩阵N，它的ij项是:

上一篇：“数学帝”葛军坦言：数学好的孩子，多半有这
下一篇：没有了