数学学习的核心之一，就是掌握数形结合思想，

数形结合思想是数学解题当中最常用、最重要的数学思想方法之一，也是中学数学教育中最常见数学思想之一。运用数形结合思想，我们可以使某些抽象的数学问题变得更加直观化、生动化，能够让抽象思维转化成形象思维，有助于我们把握数学问题的本质，这样便使很多数学问题迎刃而解，让“难懂”解法变的容易理解和消化。

数形结合思想是指从几何直观角度，利用几何图形的性质研究数量关系，寻找代数问题的解决途径，或利用数量关系来研究几何图形的性质、解决几何问题的一种数学思想。因此，数形结合思想的实质是将抽象的数学语言与直观的图像结合起来，关键是代数问题与图形之间的相互转化。

数形结合思想就是一种非常重要的数学思想，也是中学数学教育中最常见数学思想之一。数形结合思想是指从几何直观角度，利用几何图形的性质研究数量关系，寻找代数问题的解决途径，或利用数量关系来研究几何图形的性质、解决几何问题的一种数学思想。

其实质是将抽象的数学语言与直观的图象结合起来，关键是代数问题与图形之间的相互转化。

数形结合思想有关的中考试题分析，典型例题1：

如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA．

（1）求△OAB的面积；

（2）若抛物线y=-x2-2x+c经过点A．

①求c的值；

②将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围（直接写出答案即可）．

考点分析：

二次函数综合题；代数几何综合题；数形结合．

题干分析：

（1）根据点A的坐标是（-2，4），得出AB，BO的长度，

即可得出△OAB的面积；

（2）①把点A的坐标（-2，4）代入y=-x2-2x+c中，直接得出即可；

②利用配方法求出二次函数解析式即可得出顶点坐标，

根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围．

解题反思：

此题主要考查了二次函数的综合应用以及二次函数顶点坐标求法，二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握．

数形结合思想有关的中考试题分析，典型例题2：

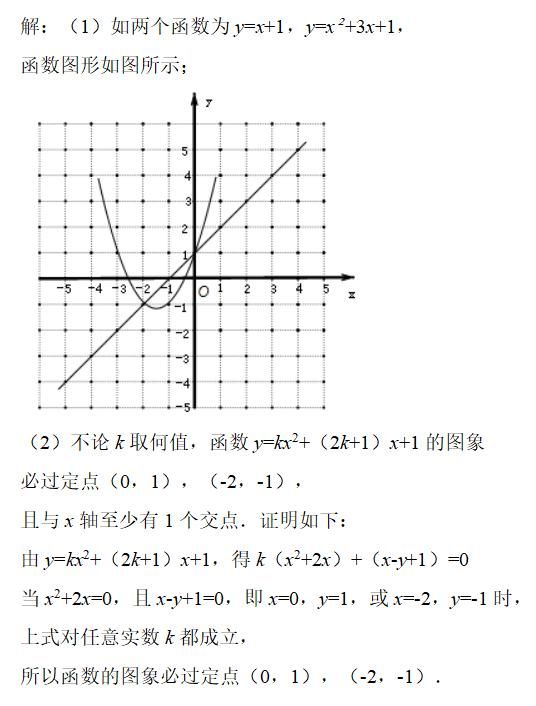
设函数y=kx2+（2k+1）x+1（k为实数）

（1）写出其中的两个特殊函数，使它们的图象不全是抛物线，并在同一直角坐标系中，用描点法画出这两个特殊函数的图象；

（2）根据所画图象，猜想出：对任意实数k，函数的图象都具有的特征，并给予证明；

（3）对任意负实数k，当x＜m时，y随着x的增大而增大，试求出m的一个值．

考点分析：

二次函数综合题；综合题；数形结合．

题干分析：

（1）令k=0或1，分别得到两个特殊函数，画出图象即可；

（2）猜想：不论k取何值，函数y=kx+（2k+1）x+1的图象必过定点（0，1），（-2，-1）．由解析式变形，得y=k（x2+2x）+（x+1），可知当x2+2x=0，即x=0或-2时，函数值与k的取值无关，此时y=1或-1，可得定点坐标；

（3）只求m的一个值即可．当k＜0时，抛物线对称轴为直线x=-（2k+1）/2k，在对称轴左侧，y随x的增大而增大，根据题意，得m≤-（2k+1）/2，而当k＜0时，-（2k+1）/2=-1-1/2k＞-1，可确定m的范围，在范围内取m的一个值即可．

解题反思：

本题主要考查了二次函数解析式的确定、函数图象交点的求法、二次函数的增减性等知识点．主要考查学生数形结合的数学思想方法．

数形结合思想有关的中考试题分析，典型例题3：

在直角坐标系xoy中，已知点P是反比例函数y=2√3/x（x＞0）图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．

（1）如图1，⊙P运动到与x轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．

（2）如图2，⊙P运动到与x轴相交，设交点为B，C．当四边形ABCP是菱形时：

①求出点A，B，C的坐标．

②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的1/2．若存在，试求出所有满足条件的M点的坐标，若不存在，试说明理由．

上一篇：高考数学仅考15分，清华校长看试卷后，却激动拍
下一篇：没有了